One of the advantages of using MCCV is it’s data-driven approach. Given data, you can answer questions such as:
How predictive is Y from X?
Is a certain cut of the data driving the prediction?
Is there another variable obscuring or influencing the contribution of X in predicting Y?
In this article I want to illustrate another type of question MCCV can address:
How does the prediction of Y by X compare to the prediction by X to a random Y? In other words, what is the power of my data X to predict Y?
I will discuss at the end how the term ‘power’ is used here in comparison to the statistical and more common form of the term. First, I will show two examples showing the power of X to predict Y.
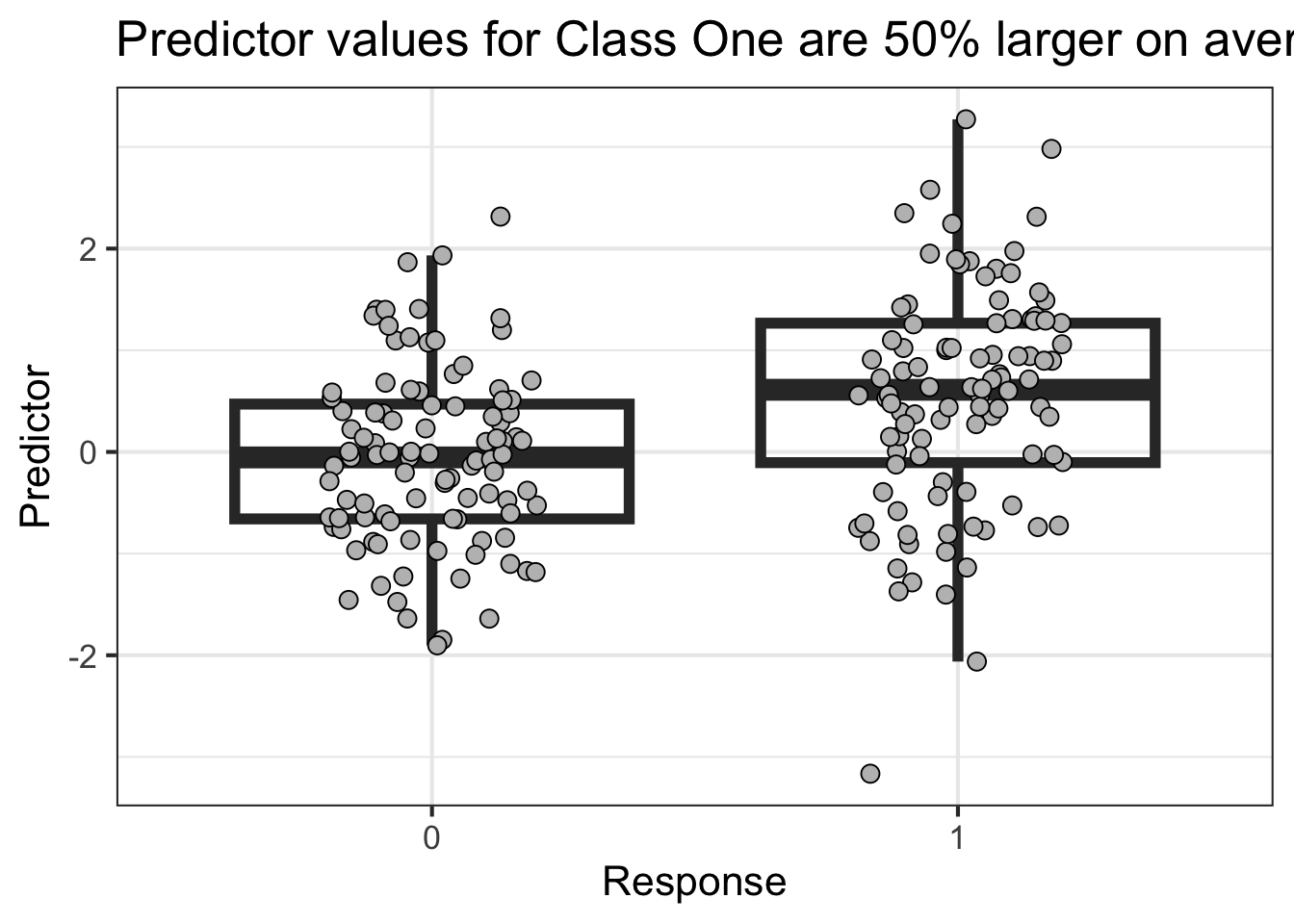
This first example shows low power
Show The Code
import numpy as np= 100 = np.random.normal(loc= 0 ,scale= 1 ,size= N)= np.random.normal(loc= 0.5 ,scale= 1 ,size= N)= np.concatenate([X1,X2])= np.concatenate([np.repeat(0 ,N),np.repeat(1 ,N)])import pandas as pd= pd.DataFrame(data= {'Y' : Y,'X' : X})= 'pt'
Show The Code
library (tidyverse)<- reticulate:: py$ df'Y' ]] <- factor (df$ Y,levels= c (0 ,1 ))%>% ggplot (aes (Y,X)) + geom_boxplot (outlier.size = NA ,alpha= 0 ,linewidth= 2 ) + geom_point (position = position_jitter (width = .2 ),pch= 21 ,fill= 'gray' ,size= 3 ) + labs (x = "Response" ,y= "Predictor" ,title = "Predictor values for Class One are 50% larger on average" ) + theme_bw (base_size = 16 )
Show The Code
import mccv= mccv.mccv(num_bootstraps= 200 ,n_jobs= 4 )'X' ]])'Y' ]])'Feature Importance' ].insert(len (mccv_obj.mccv_data['Feature Importance' ].columns),'type' ,'real' 'Model Learning' ].insert(len (mccv_obj.mccv_data['Model Learning' ].columns),'type' ,'real' 'Patient Predictions' ].insert(len (mccv_obj.mccv_data['Patient Predictions' ].columns),'type' ,'real' 'Feature Importance' ].insert(len (mccv_obj.mccv_permuted_data['Feature Importance' ].columns),'type' ,'permuted' 'Model Learning' ].insert(len (mccv_obj.mccv_permuted_data['Model Learning' ].columns),'type' ,'permuted' 'Patient Predictions' ].insert(len (mccv_obj.mccv_permuted_data['Patient Predictions' ].columns),'type' ,'permuted' = \ 'Feature Importance' ].'feature=="X"' ).= True )),'Feature Importance' ].'feature=="X"' ).= True ))= \ 'Patient Predictions' ].'y_pred' ,axis= 1 ).'Patient Predictions' ].'y_pred' ,axis= 1 ))= \ 'Model Learning' ].'Model Learning' ].
Show The Code
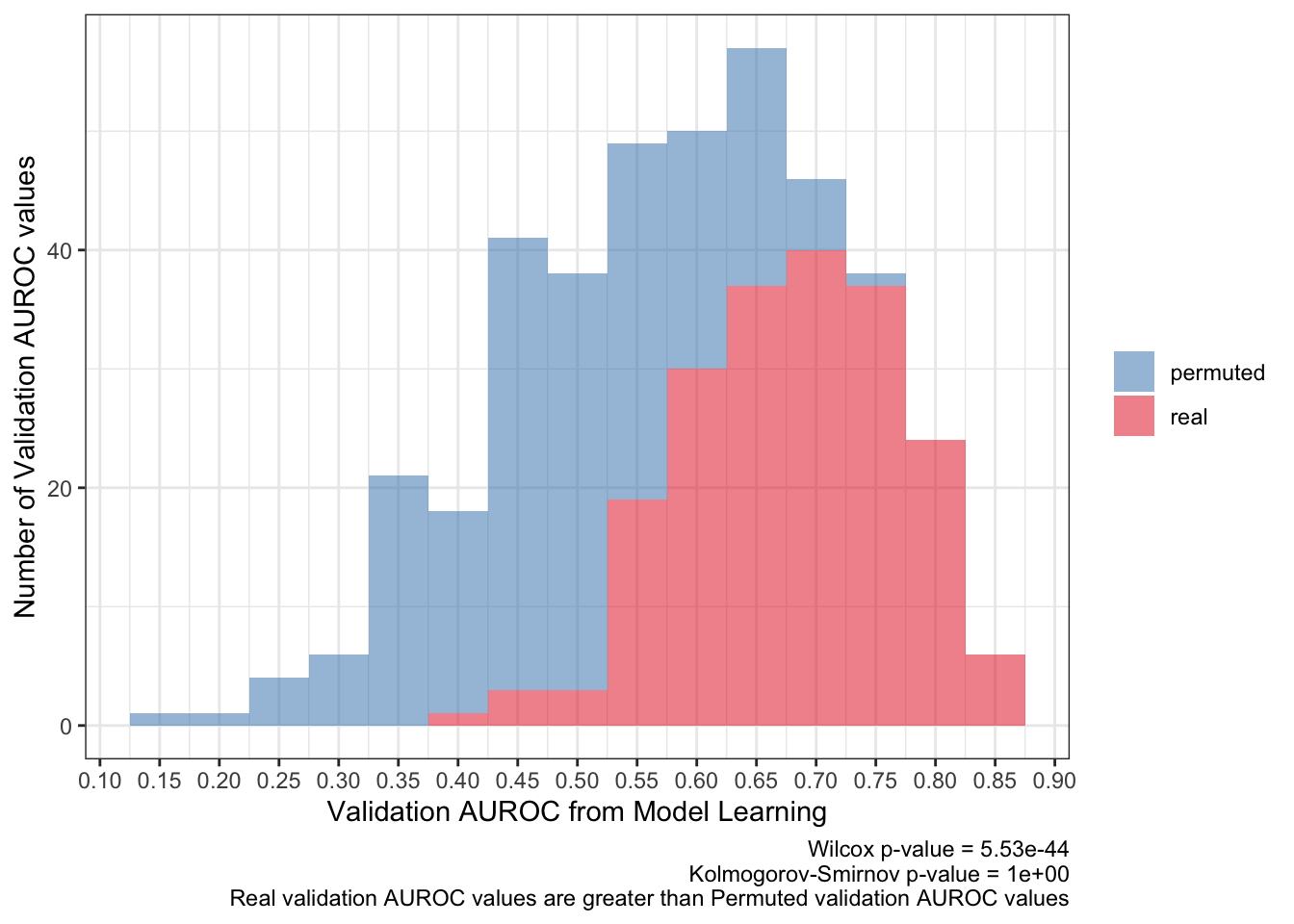
<- ks.test (:: py$ pred_df %>% filter (type== 'real' ) %>% pull (validation_roc_auc),:: py$ pred_df %>% filter (type== 'permuted' ) %>% pull (validation_roc_auc),alternative = 'greater' 'p.value' ]]<- wilcox.test (:: py$ pred_df %>% filter (type== 'real' ) %>% pull (validation_roc_auc),:: py$ pred_df %>% filter (type== 'permuted' ) %>% pull (validation_roc_auc)'p.value' ]]:: py$ pred_df %>% ggplot (aes (validation_roc_auc,fill= type)) + geom_histogram (aes (y= after_stat (count)),alpha= .5 ,binwidth = .05 ) + scale_fill_brewer (palette = 'Set1' ,direction = - 1 ,guide= guide_legend (title= NULL )) + theme_bw () + scale_x_continuous (breaks= seq (0 ,1 ,0.05 ),+ labs (x= 'Validation AUROC from Model Learning' ,y= 'Number of Validation AUROC values' ,caption= paste0 ('Wilcox p-value = ' ,scales:: scientific (pwilcox,3 ),' \n ' ,'Kolmogorov-Smirnov p-value = ' ,scales:: scientific (pks,3 ),' \n ' ,'Real validation AUROC values are greater than Permuted validation AUROC values' ))
Show The Code
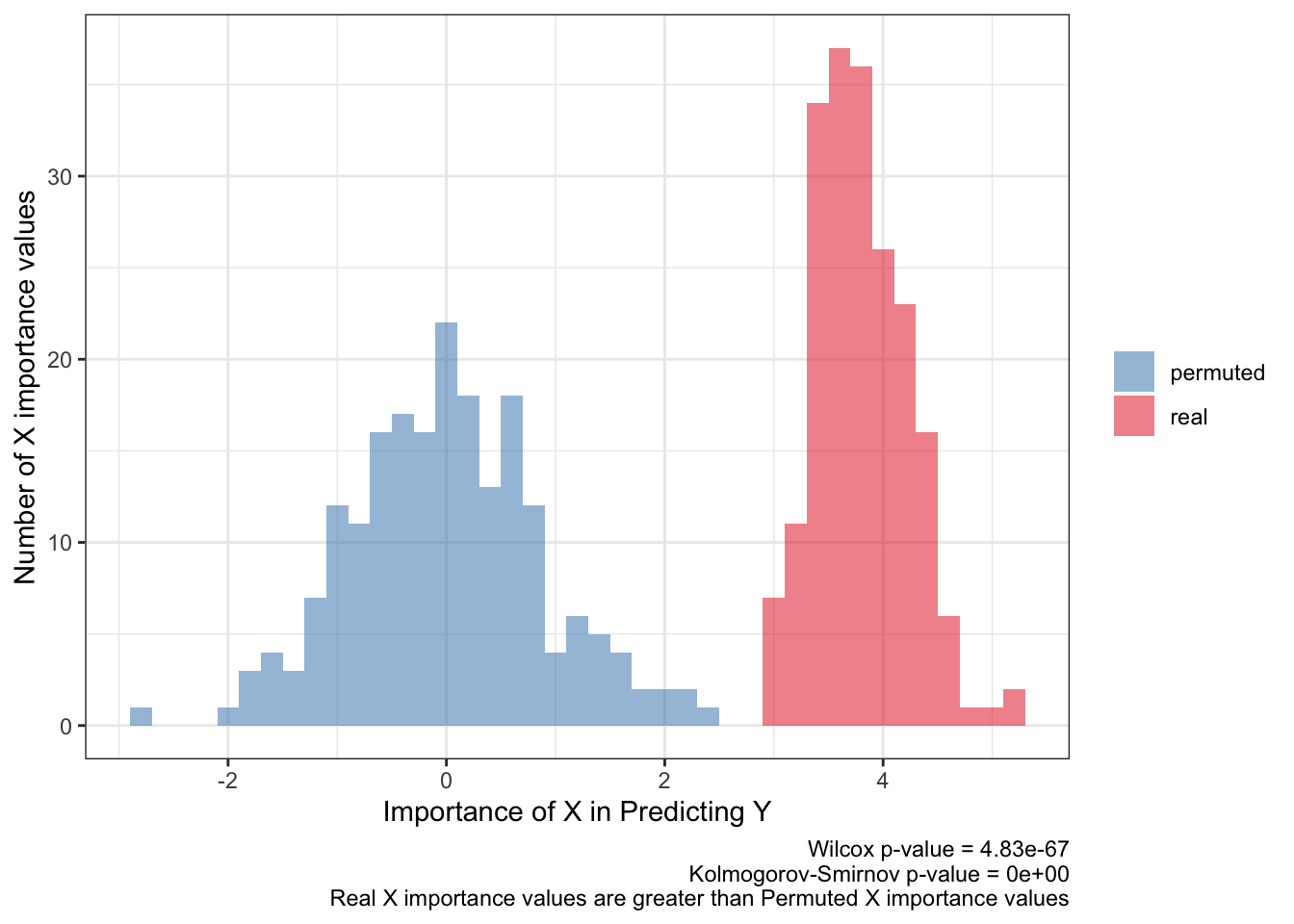
<- ks.test (:: py$ fimp_df %>% filter (type== 'real' ) %>% pull (importance),:: py$ fimp_df %>% filter (type== 'permuted' ) %>% pull (importance)'p.value' ]]<- wilcox.test (:: py$ fimp_df %>% filter (type== 'real' ) %>% pull (importance),:: py$ fimp_df %>% filter (type== 'permuted' ) %>% pull (importance)'p.value' ]]:: py$ fimp_df %>% ggplot (aes (importance,fill= type)) + geom_histogram (aes (y= after_stat (count)),alpha= .5 ,binwidth = .2 ) + scale_fill_brewer (palette = 'Set1' ,direction = - 1 ,guide= guide_legend (title= NULL )) + theme_bw () + labs (x= 'Importance of X in Predicting Y' ,y= 'Number of X importance values' ,caption= paste0 ('Wilcox p-value = ' ,scales:: scientific (pwilcox,3 ),' \n ' ,'Kolmogorov-Smirnov p-value = ' ,scales:: scientific (pks,3 ),' \n ' ,'Real X importance values are greater than Permuted X importance values' ))
Show The Code
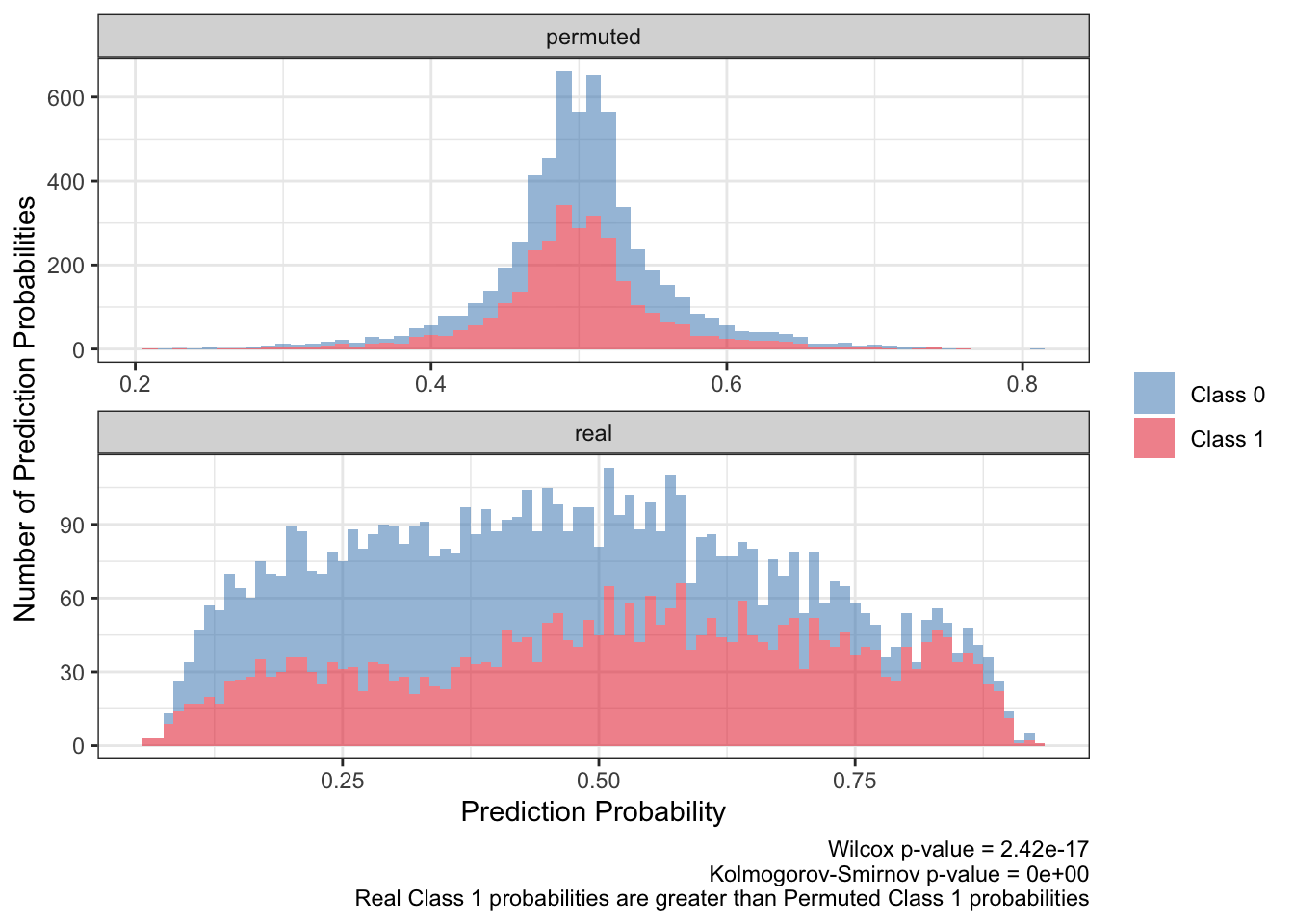
<- ks.test (:: py$ ppred_df %>% filter (type== 'real' & y_true== 1 ) %>% pull (y_proba),:: py$ ppred_df %>% filter (type== 'permuted' & y_true== 1 ) %>% pull (y_proba)'p.value' ]]<- wilcox.test (:: py$ ppred_df %>% filter (type== 'real' & y_true== 1 ) %>% pull (y_proba),:: py$ ppred_df %>% filter (type== 'permuted' & y_true== 1 ) %>% pull (y_proba)'p.value' ]]:: py$ ppred_df %>% arrange (pt,bootstrap) %>% ggplot (aes (y_proba,fill= factor (y_true),group= y_true)) + geom_histogram (aes (y= after_stat (count)),alpha= .5 ,binwidth = .01 ) + scale_fill_brewer (NULL ,palette = 'Set1' ,direction = - 1 ,labels= c ("Class 0" ,"Class 1" ),guide= guide_legend (title= NULL )) + facet_wrap (~ type,ncol= 1 ,scales= 'free' ) + theme_bw () + labs (x= 'Prediction Probability' ,y= 'Number of Prediction Probabilities' ,caption = paste0 ('Wilcox p-value = ' ,scales:: scientific (pwilcox,3 ),' \n ' ,'Kolmogorov-Smirnov p-value = ' ,scales:: scientific (pks,3 ),' \n ' ,'Real Class 1 probabilities are greater than Permuted Class 1 probabilities' ))
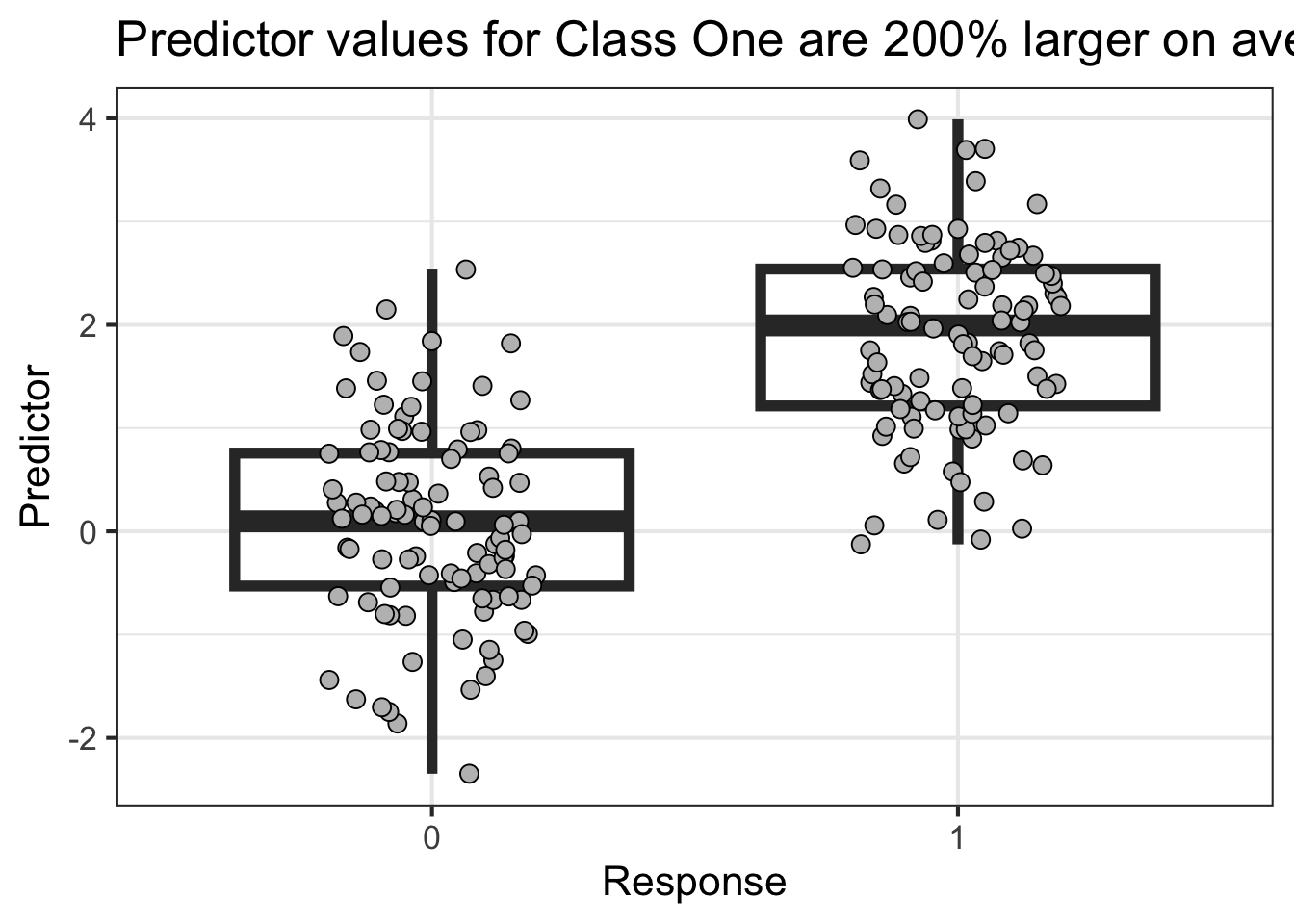
This next example shows high power
Show The Code
import numpy as np= 100 = np.random.normal(loc= 0 ,scale= 1 ,size= N)= np.random.normal(loc= 2 ,scale= 1 ,size= N)= np.concatenate([X1,X2])= np.concatenate([np.repeat(0 ,N),np.repeat(1 ,N)])import pandas as pd= pd.DataFrame(data= {'Y' : Y,'X' : X})= 'pt'
Show The Code
library (tidyverse)<- reticulate:: py$ df'Y' ]] <- factor (df$ Y,levels= c (0 ,1 ))%>% ggplot (aes (Y,X)) + geom_boxplot (outlier.size = NA ,alpha= 0 ,linewidth= 2 ) + geom_point (position = position_jitter (width = .2 ),pch= 21 ,fill= 'gray' ,size= 3 ) + labs (x = "Response" ,y= "Predictor" ,title = "Predictor values for Class One are 200% larger on average" ) + theme_bw (base_size = 16 )
Show The Code
import mccv= mccv.mccv(num_bootstraps= 200 ,n_jobs= 4 )'X' ]])'Y' ]])'Feature Importance' ].insert(len (mccv_obj.mccv_data['Feature Importance' ].columns),'type' ,'real' 'Model Learning' ].insert(len (mccv_obj.mccv_data['Model Learning' ].columns),'type' ,'real' 'Patient Predictions' ].insert(len (mccv_obj.mccv_data['Patient Predictions' ].columns),'type' ,'real' 'Feature Importance' ].insert(len (mccv_obj.mccv_permuted_data['Feature Importance' ].columns),'type' ,'permuted' 'Model Learning' ].insert(len (mccv_obj.mccv_permuted_data['Model Learning' ].columns),'type' ,'permuted' 'Patient Predictions' ].insert(len (mccv_obj.mccv_permuted_data['Patient Predictions' ].columns),'type' ,'permuted' = \ 'Feature Importance' ].'feature=="X"' ).= True )),'Feature Importance' ].'feature=="X"' ).= True ))= \ 'Patient Predictions' ].'y_pred' ,axis= 1 ).'Patient Predictions' ].'y_pred' ,axis= 1 ))= \ 'Model Learning' ].'Model Learning' ].
Show The Code
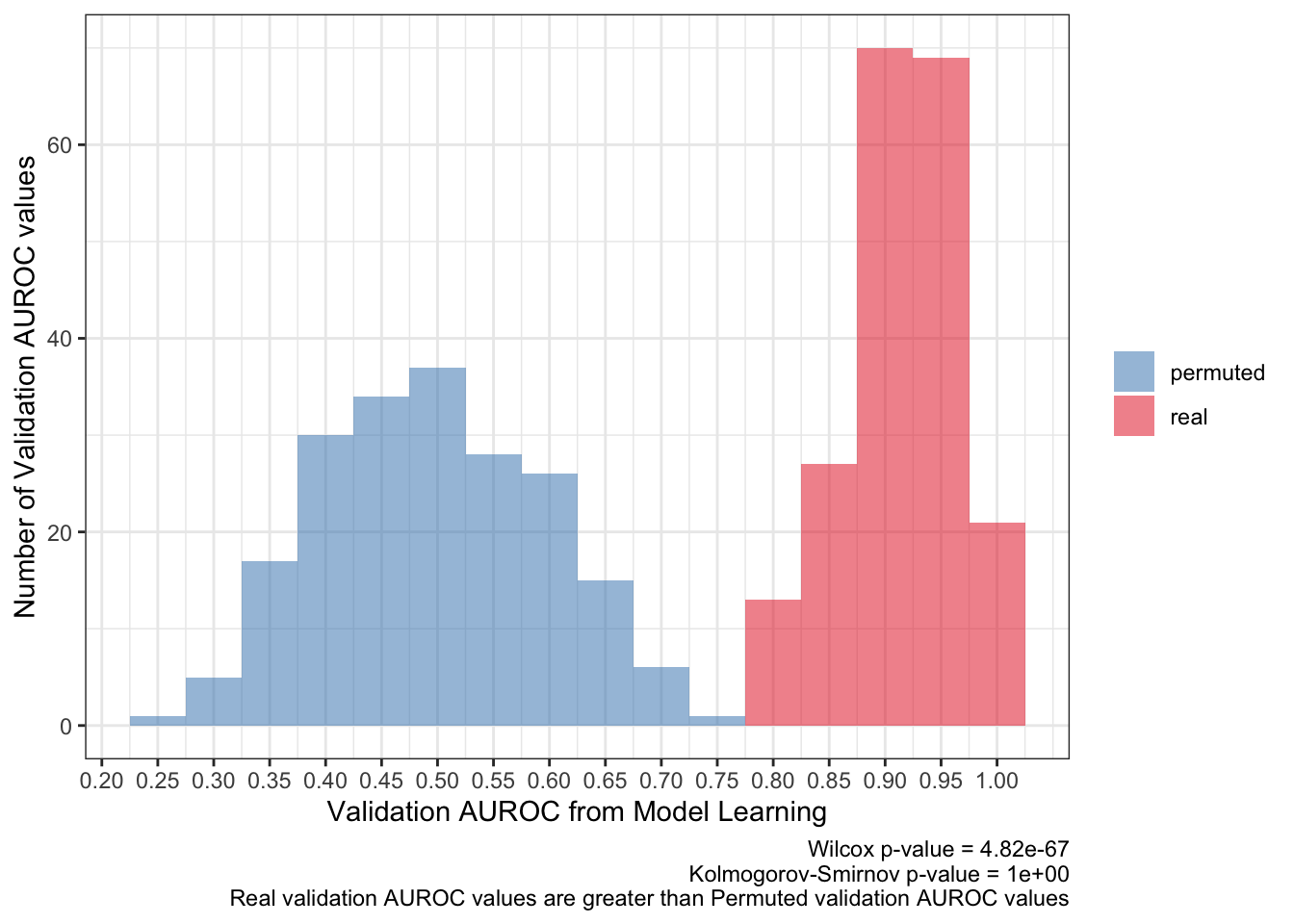
<- ks.test (:: py$ pred_df %>% filter (type== 'real' ) %>% pull (validation_roc_auc),:: py$ pred_df %>% filter (type== 'permuted' ) %>% pull (validation_roc_auc),alternative = 'greater' 'p.value' ]]<- wilcox.test (:: py$ pred_df %>% filter (type== 'real' ) %>% pull (validation_roc_auc),:: py$ pred_df %>% filter (type== 'permuted' ) %>% pull (validation_roc_auc)'p.value' ]]:: py$ pred_df %>% ggplot (aes (validation_roc_auc,fill= type)) + geom_histogram (aes (y= after_stat (count)),alpha= .5 ,binwidth = .05 ) + scale_fill_brewer (palette = 'Set1' ,direction = - 1 ,guide= guide_legend (title= NULL )) + theme_bw () + scale_x_continuous (breaks= seq (0 ,1 ,0.05 ),+ labs (x= 'Validation AUROC from Model Learning' ,y= 'Number of Validation AUROC values' ,caption= paste0 ('Wilcox p-value = ' ,scales:: scientific (pwilcox,3 ),' \n ' ,'Kolmogorov-Smirnov p-value = ' ,scales:: scientific (pks,3 ),' \n ' ,'Real validation AUROC values are greater than Permuted validation AUROC values' ))
Show The Code
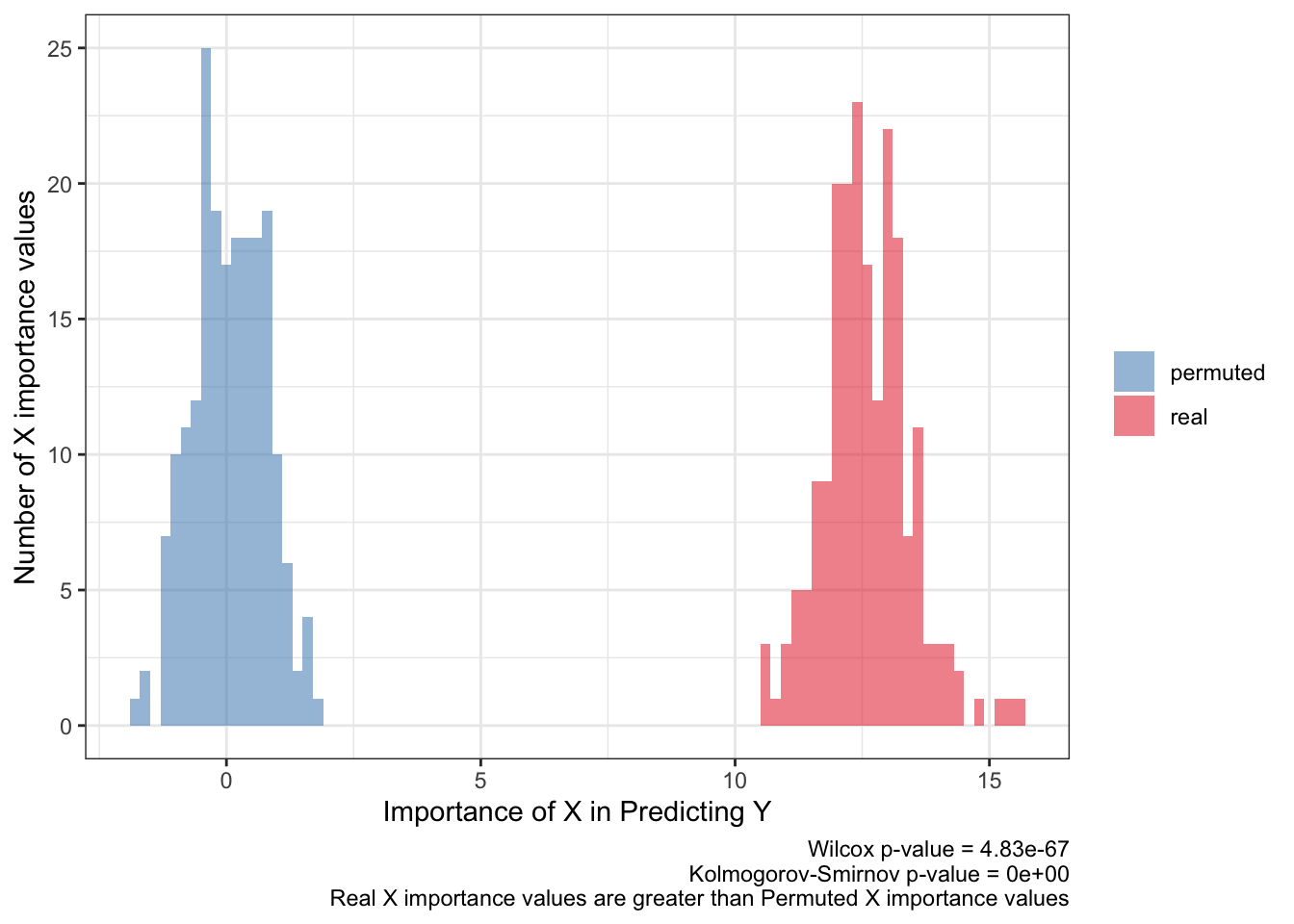
<- ks.test (:: py$ fimp_df %>% filter (type== 'real' ) %>% pull (importance),:: py$ fimp_df %>% filter (type== 'permuted' ) %>% pull (importance)'p.value' ]]<- wilcox.test (:: py$ fimp_df %>% filter (type== 'real' ) %>% pull (importance),:: py$ fimp_df %>% filter (type== 'permuted' ) %>% pull (importance)'p.value' ]]:: py$ fimp_df %>% ggplot (aes (importance,fill= type)) + geom_histogram (aes (y= after_stat (count)),alpha= .5 ,binwidth = .2 ) + scale_fill_brewer (palette = 'Set1' ,direction = - 1 ,guide= guide_legend (title= NULL )) + theme_bw () + labs (x= 'Importance of X in Predicting Y' ,y= 'Number of X importance values' ,caption= paste0 ('Wilcox p-value = ' ,scales:: scientific (pwilcox,3 ),' \n ' ,'Kolmogorov-Smirnov p-value = ' ,scales:: scientific (pks,3 ),' \n ' ,'Real X importance values are greater than Permuted X importance values' ))
Show The Code
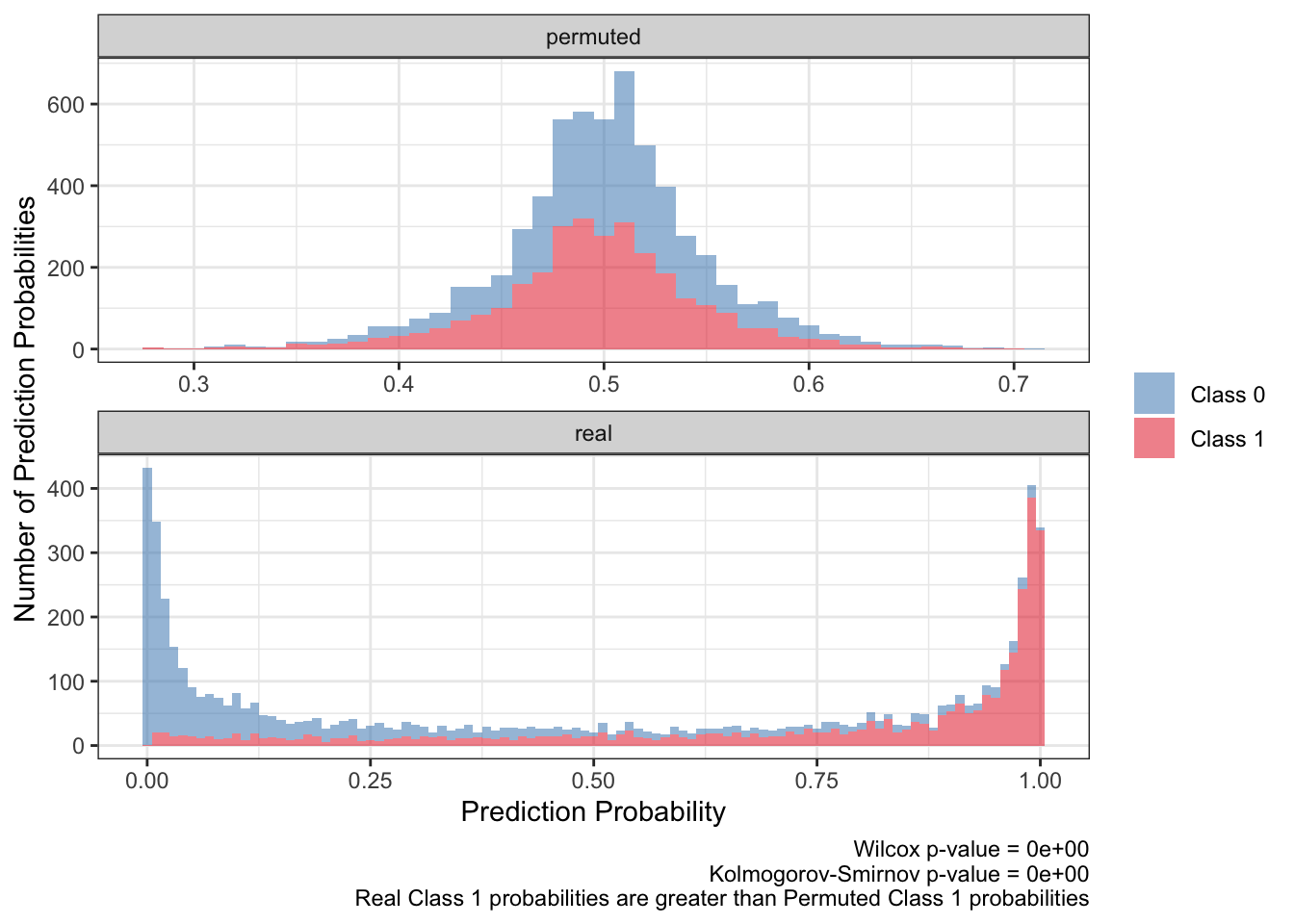
<- ks.test (:: py$ ppred_df %>% filter (type== 'real' & y_true== 1 ) %>% pull (y_proba),:: py$ ppred_df %>% filter (type== 'permuted' & y_true== 1 ) %>% pull (y_proba)'p.value' ]]<- wilcox.test (:: py$ ppred_df %>% filter (type== 'real' & y_true== 1 ) %>% pull (y_proba),:: py$ ppred_df %>% filter (type== 'permuted' & y_true== 1 ) %>% pull (y_proba)'p.value' ]]:: py$ ppred_df %>% arrange (pt,bootstrap) %>% ggplot (aes (y_proba,fill= factor (y_true),group= y_true)) + geom_histogram (aes (y= after_stat (count)),alpha= .5 ,binwidth = .01 ) + scale_fill_brewer (NULL ,palette = 'Set1' ,direction = - 1 ,labels= c ("Class 0" ,"Class 1" ),guide= guide_legend (title= NULL )) + facet_wrap (~ type,ncol= 1 ,scales= 'free' ) + theme_bw () + labs (x= 'Prediction Probability' ,y= 'Number of Prediction Probabilities' ,caption = paste0 ('Wilcox p-value = ' ,scales:: scientific (pwilcox,3 ),' \n ' ,'Kolmogorov-Smirnov p-value = ' ,scales:: scientific (pks,3 ),' \n ' ,'Real Class 1 probabilities are greater than Permuted Class 1 probabilities' ))
These two examples show different metrics for defining a ‘powerful’ prediction. Here, a powerful prediction can only be defined by the combination of different components to describe how and to what degree a predictor X can predict a response Y. These components can come from the model learning process as well as the applying the model on new data i.e. a validation set. Defining a powerful prediction is difficult using only one quantitative metric, like the statistical tests shown in the plot captions. But a few metrics noted here (and probably others I’ve mistakingly overlooked) can accurately define a powerful prediction:
The average AUROC for the validation set should be more than 50%. To be more strict, the 95% confidence interval should be greater than 50% AUROC.
The importance value (beta coefficient for logistic regression) of X for predicting Y should be above the null association i.e. 0 and should barely overlap the importance values for a shuffled response. Statistical tests will probably produce a false positive by showing a small p-value, like here, so they shouldn’t be the metric in defining a powerful prediction.
There seems to be at least two takeaways from the distributions of the prediction probabilities. First, the distribution of the real predicted probabilities for class 1 need to be greater than that for class 0. Also the distribution of real, class 1 predicted probabilities need to be greater than the distribution of permuted, class 1 predicted probabilities.
I used a combination of the metrics referenced above in the papers published using MCCV. This article’s toy examples illustrate why these metrics are sensible for defining the power of a prediction given the data.