Getting Started

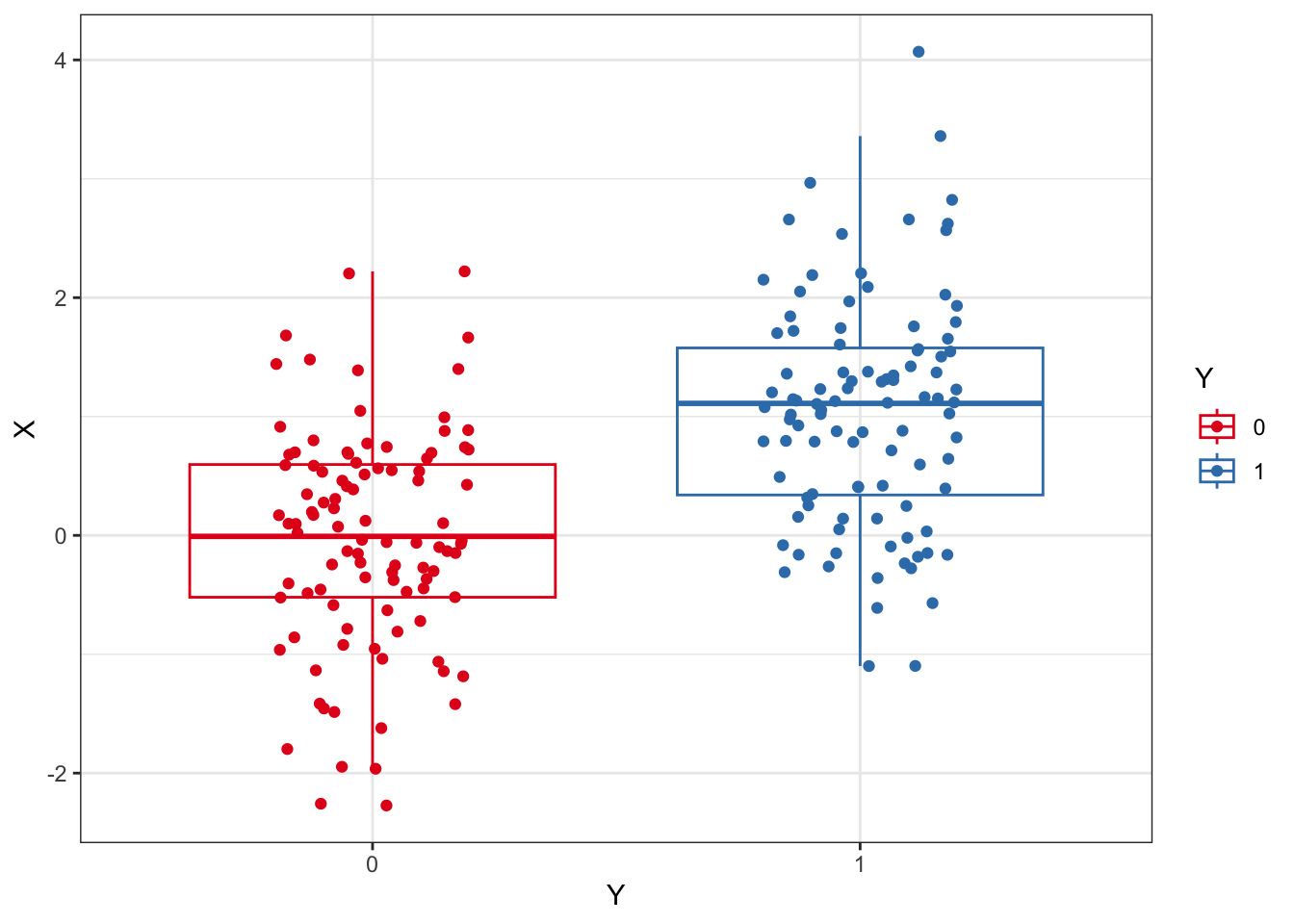
We start out with a dataset where we want to evaluate an outcome, Y, to be predicted by an independent variable, X. In this example, X determines Y and so we expect Y to be predicted by X to some degree. MCCV can be used to quantify that prediction. We’ll refer to the observations as patients, as you can view the dataset applying to patients experiencing an outcome during or at the end of a clinical trial.

Below, I’m demonstrating how I would go between Python and R, but you can stay solely in R or Python.

Generate a Dataset: Binary outcome Y and independent variable(s) X

Show The Code 

import numpy as np
N=100
X1 = np.random.normal(loc=0,scale=1,size=N)
X2 = np.random.normal(loc=1,scale=1,size=N)
X = np.concatenate([X1,X2])
Y = np.concatenate([np.repeat(0,N),np.repeat(1,N)])
Show The Code 
df <- 
    tibble::tibble(
        X = reticulate::py$X,
        Y = reticulate::py$Y
        )
df[['Y']] <- factor(df$Y,levels=c(0,1))

library(ggplot2)
ggplot(data=df,mapping=aes(Y,X,color=Y)) +
    geom_boxplot(alpha=0) +
    geom_point(position=position_jitter(width=0.2)) +
    scale_color_brewer(palette="Set1") +
    theme_bw()

Employ MCCV: Predict Y from X

Show The Code 
import pandas as pd
df = pd.DataFrame(data={'X' : X,'Y' : Y})
df.index.name = 'pt'

X = df.loc[:,['X']]
Y = df.loc[:,['Y']]
Show The Code 
import mccv
mccv_obj = mccv.mccv(num_bootstraps=200,n_jobs=2)
mccv_obj.set_X(X)
mccv_obj.set_Y(Y)
mccv_obj.run_mccv()
Show The Code 
ml_df = mccv_obj.mccv_data['Model Learning']
f_imp_df = mccv_obj.mccv_data['Feature Importance']
preds_df = mccv_obj.mccv_data['Performance']
pt_preds_df = (
    mccv_obj.mccv_data['Patient Predictions'].
    reset_index()
    )

Visualize prediction results

Show The Code 
library(magrittr)
p1 <- reticulate::py$ml_df %>% 
    tidyr::pivot_longer(
        cols = dplyr::contains('roc')
    ) %>% 
    dplyr::mutate(
        name = factor(name,levels=c(
            "train_roc_auc","test_roc_auc",
            "validation_roc_auc"
        ))
    ) %>% 
    ggplot(aes(model,value,color=name)) +
    geom_boxplot(alpha=0) +
    geom_point(aes(group=name),
               position=position_jitterdodge(
                   dodge.width = 0.7,
                   jitter.width = 0.1
                   )
               ) +
    scale_color_brewer(palette="Set1") +
    scale_y_continuous(limits=c(0,1)) +
    theme_bw() +
    labs(title="Model performance results")
p2 <- reticulate::py$f_imp_df %>% 
    ggplot(aes(feature,importance,color=feature)) +
    geom_boxplot(alpha=0) +
    geom_point(position=position_jitter(width=0.2)) +
    scale_color_brewer(palette="Set2") +
    theme_bw() +
    labs(title="Model feature importance results")
Warning in py_to_r.pandas.core.frame.DataFrame(x): index contains duplicated
values: row names not set
Show The Code 
p3 <- reticulate::py$preds_df %>% 
    ggplot(aes(metric,value)) +
    geom_boxplot(alpha=0) +
    geom_point(pch=21,
               position=position_jitter(width=0.2)) +
    theme_bw() +
    labs(title="Model validation predictions",
         subtitle="From bootstrap of patient probabilities")
p4 <- reticulate::py$pt_preds_df %>% 
    dplyr::mutate(
        y_true = factor(y_true,levels=c(0,1))
    ) %>% 
    dplyr::group_by(bootstrap,model,y_true) %>% 
    dplyr::summarise(
        mean_y_proba = mean(y_proba),
        .groups = "drop"
    ) %>% 
    ggplot(aes(y_true,mean_y_proba,color=y_true)) +
    geom_boxplot(alpha=0) +
    geom_point(position=position_jitter(width=0.2)) +
    scale_color_manual(values=c("orange","purple")) +
    facet_wrap(~model) +
    scale_y_continuous(limits=c(0,1)) +
    theme_bw() +
    labs(title="Patient class predictions",
         subtitle="Average of bootstrap probabilities per patient")

library(patchwork)
p1 + p2 + p3 + p4 + plot_layout(ncol = 2)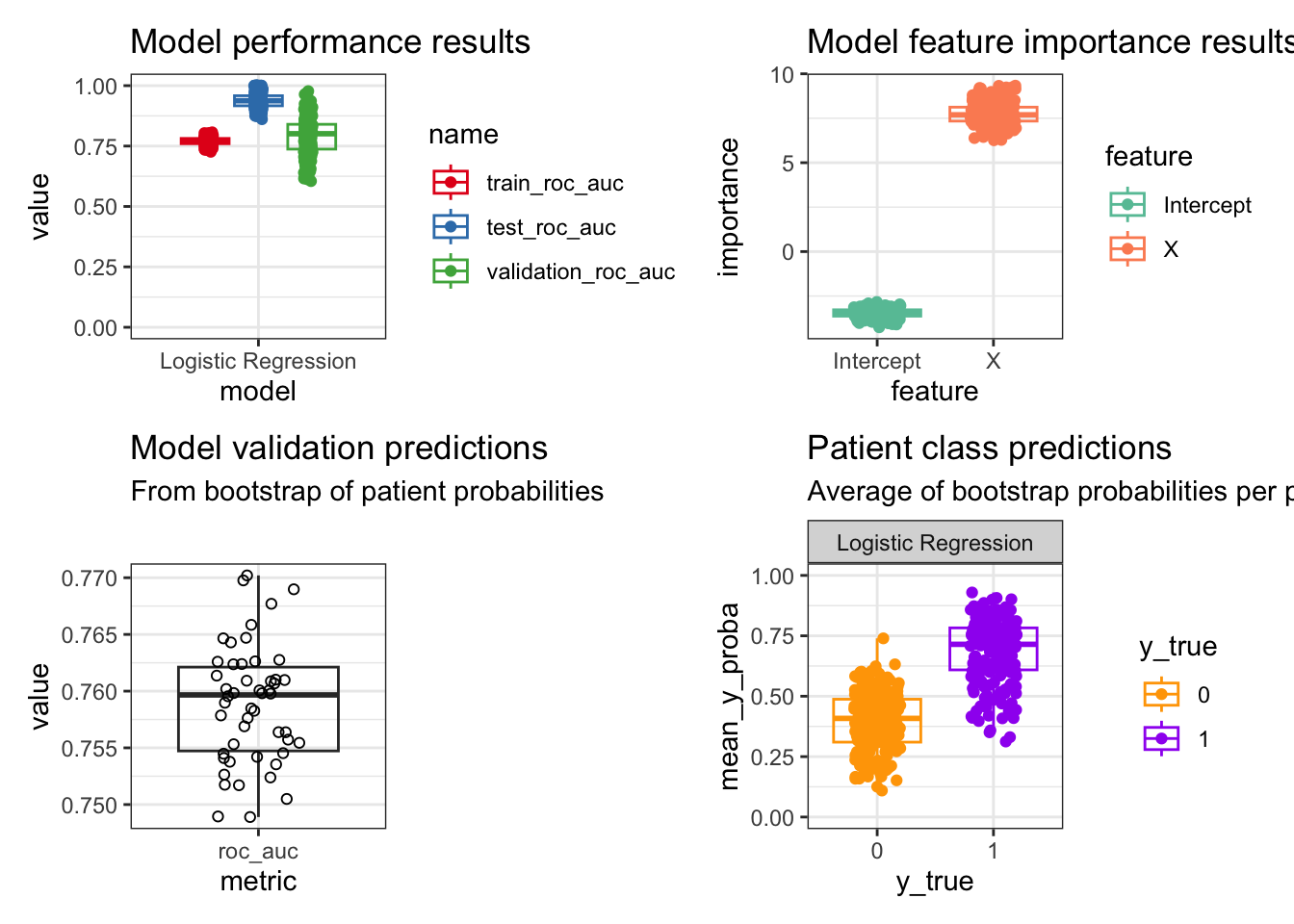

These plots are an overview to the main results generated by this algorithm:

  1. The performance of the model, across the bootstraps, during training and testing (within 10 fold cross validation) and also validation on the unseen patients.
  2. The coefficients or importances quantified by the model fit on the entire training (train+test from above) dataset after the 10-fold cross validation for hyperparameter tuning.
  3. The model validation predictions derived by bootstrapping (N=50) the resulting patient probabilities.
  4. The predicted patient probabilities compared to the true patient classes or outcomes. Here, the probabilities were averaged per patient across the bootstraps.

Interpreting MCCV predictions

Some observations from this small example:

  • As expected, the testing performance is much higher than the model training performance. The model validation performance has more variance.

  • Y is directly derived from X and so we see a large importance for X in predicting Y. The intercept doesn’t have much meaning in this contrived example, but could be meaningful depending on the dataset.

  • The performance after bootstrapping the patient probabilities has less variance compared to the first graph, but is within the middle 50% of that distribution. This performance measure should be used because it has reduced bias from sampling all computed patient probabilities.

  • The average patient probabilities across bootstraps show the average prediction by that classifier on an individual basis, as well as the per patient variance. This allows for examining further how variable a model can be for certain patient subpopulations for the classification task.

Go further with MCCV

  • You can compute random permutations in order to compare your ‘observed’ model to just randomly shuffling your data. You can make similar plots with data from the method run_permuted_mccv:
Show The Code 
mccv_obj.run_permuted_mccv()

  • See the model evaluations and validations in these references for some ideas like model calibration and deriving model equations: